11153. Kefa and park
Kefa decided to celebrate his first big
salary by going to a restaurant.
He lives near an unusual park. The park is
a rooted tree with n vertices, rooted at vertex 1. Kefa’s
house is located at vertex 1 as well. Unfortunately for our hero, the
park is inhabited by cats, and Kefa has already identified the vertices where
the cats are located.
The leaf vertices of the park contain restaurants. Kefa wants to choose a restaurant, but
he is very afraid of cats. Therefore, he will not go to a restaurant if, on the
path from his house to the restaurant, he encounters more than m consecutive
vertices with cats.
Your task is to help Kefa count the number
of restaurants he can safely visit.
Input. The first line contains two integers n and m (2 ≤ n ≤ 105, 1
≤ m ≤ n) – the number of vertices in the tree and the maximum number of
consecutive vertices with cats that Kefa can tolerate.
The second line contains n integers a1, a2, ..., an, where each ai is
either 0 (there is no cat at vertex i) or 1 (there
is a cat at vertex i).
The following n – 1 lines contains
the tree’s edges in the format xi yi (1 ≤ xi, yi
≤ n, xi ≠ yi), where xi and yi are vertices connected by an edge.
It is guaranteed that this set of edges
forms a tree.
Output. Print the number of leaf vertices that Kefa can reach
if there are no more than m consecutive vertices with cats on
the way from his house.
|
Sample
input 1 |
Sample
output 1 |
|
7 1 1 1 0 0 0 0 1 1 2 1 3 2 4 2 5 3 6 3 7 |
2 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
8 2 1 1 0 1 0 1 0 1 1 2 2 3 2 5 2 6 3 4 6 7 6 8 |
2 |
SOLUTION
tree
Algorithm analysis
Start a depth first search from vertex 1, where Kefa’s house is
located. One of the parameters of the dfs function will store the
number of consecutive vertices with cats. If at vertex v this number
exceeds m, we’ll not continue the depth-first search from this vertex.
We count the number of visited leaf vertices. A vertex
is a leaf if its degree is 1 and it is not a root (vertex 1).
Example
Let’s consider the trees from
the first and second examples.
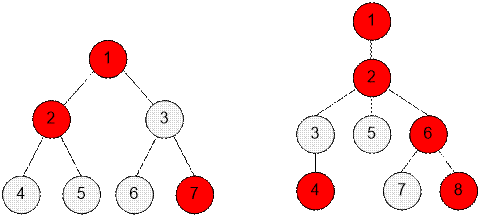
In
the first example, Kefa can pass through only one consecutive vertex with a
cat. He will be able to reach the restaurants located at vertices 6 and 7.
In
the second example, Kefa can pass through two consecutive vertices with cats.
He will be able to reach the restaurants located at vertices 4 and 5.
Algorithm implementation
The
location of the cats is stored in the array cats. The tree is stored in
the adjacency list g.
vector<int> cats;
vector<vector<int> > g;
The dfs
function performs a depth-first search from vertex v and returns the
number of restaurants that can be reached from this vertex (under the condition
that no more than m consecutive vertices with cats are encountered on
the path to them). The parent of vertex v is the vertex prev. The
number of consecutive vertices with cats encountered up to and including vertex
v is cnt.
int dfs(int v, int prev, int cnt)
{
If more
than m consecutive cats are already encountered, further depth-first
search from vertex v is not continued.
if (cnt > m) return 0;
If we are
at a leaf, increase the number of accessible restaurants.
if (g[v].size() == 1 && prev != -1) return 1;
In the
variable res count the number of restaurants reachable
from vertex v.
int res = 0;
Iterate
over all edges (v, to) originating from vertex v. If the
vertex to is a parent of v, do not move to this vertex.
for (int to : g[v])
if (to != prev)
{
If there is
no cat at the vertex v, set c = 0. Otherwise, assign c = cnt
+ 1. The variable c stores the number of consecutive vertices with cats
up to and including vertex to.
int c = (cats[to] == 0) ? 0 : cnt + 1;
Start a
depth-first search from vertex to.
res += dfs(to, v, c);
}
Return the
result.
return res;
}
The main
part of the program. Read the input data.
scanf("%d %d", &n, &m);
cats.resize(n
+ 1);
for (i = 1; i <= n; i++)
scanf("%d", &cats[i]);
Construct a
tree.
g.resize(n
+ 1);
for (i = 1; i < n; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Print the
result. The dfs function, called from
vertex 1, returns the answer to the problem. Since vertex 1 has no parent, we
pass the value -1 as the second parameter. Starting from vertex 1, we have
encountered cats[1] cats.
printf("%d\n", dfs(1, -1, cats[1]));
Python implementation
The dfs
function performs a depth-first search from vertex v and returns the
number of restaurants that can be reached from this vertex (under the condition
that no more than m consecutive vertices with cats are encountered on
the path to them). The parent of vertex v is the vertex prev. The
number of consecutive vertices with cats encountered up to and including vertex
v is cnt.
def dfs(v, prev, cnt):
If more
than m consecutive cats are already encountered, further depth-first
search from vertex v is not continued.
if cnt > m:
return 0
If we are
at a leaf, increase the number of accessible restaurants.
if len(g[v]) == 1 and prev != -1:
return 1
In the
variable res count the number of restaurants reachable
from vertex v.
res = 0
Iterate
over all edges (v, to) originating from vertex v. If the
vertex to is an ancestor of v, do not move to this vertex.
for to in g[v]:
if to != prev:
If there is
no cat at the vertex v, set c = 0. Otherwise, assign c = cnt
+ 1. The variable c stores the number of consecutive vertices with cats
up to and including vertex to.
c = 0 if
cats[to] == 0 else cnt + 1
Start a
depth-first search from vertex to.
res += dfs(to, v, c)
Return the
result.
return res
The main
part of the program. Read the input data.
n, m = map(int, input().split())
cats = [0] + list(map(int, input().split()))
Construct a
tree.
g = [[] for _ in
range(n + 1)]
for _ in range(n - 1):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
Print the
result. The dfs function, called from
vertex 1, returns the answer to the problem. Since vertex 1 has no parent, we
pass the value -1 as the second parameter. Starting from vertex 1, we have
encountered cats[1] cats.
print(dfs(1, -1, cats[1]))